Otras aplicaciones geométricas | Teorema de Pitágoras

El Teorema de Pitágoras es fundamental en geometría, ya que hay muchas figuras planas en las que aparecen triángulos rectángulos o que pueden dividirse en triángulos rectángulos.

A continuación se muestran una serie de ejemplos donde se usa el Teorema de Pitágoras para obtener diferentes elementos de figuras planas.

Diagonal de un rectángulo

En un rectángulo, la diagonal forma con dos de los lados un triángulo rectángulo. Por lo tanto, si conocemos las dimensiones del rectángulo, podemos obtener la medida de su diagonal.

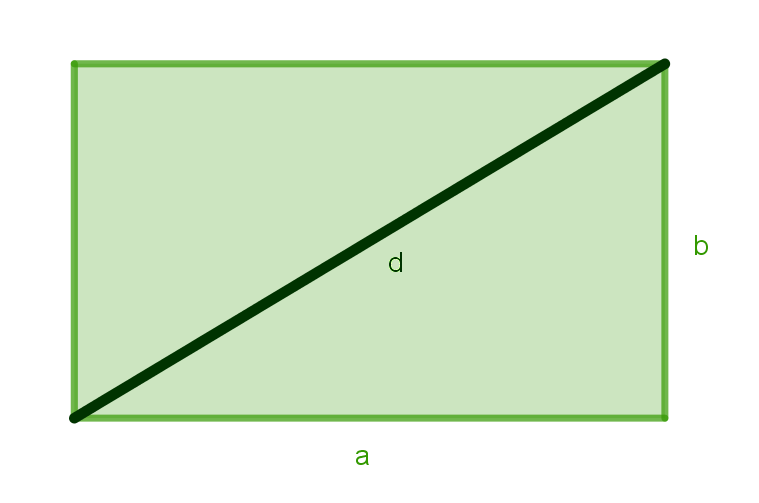
Los lados a y b se corresponden con los catetos de un triángulo rectángulo cuya hipotenusa coincide con la diagonal, d, del rectángulo. Para calcular la diagonal utilizamos el siguiente procedimiento:

d^2=a^2+b^2\rightarrow d=\sqrt{a^2+b^2}

EJEMPLO: Calcula la diagonal de un rectángulo de lados 24 cm y 10 cm.

Llamamos d a la diagonal del rectángulo, entonces por el Teorema de Pitágoras tenemos la siguiente igualdad:

d=\sqrt{24^2+10^2}=\sqrt{676}=26

Por lo tanto, la diagonal del rectángulo mide 26 cm.

Apotema de un hexágono regular

En un hexágono regular el radio mide lo mismo que el lado y, además, forma un triángulo rectángulo con la apotema y medio lado como se puede ver en la imagen.

Podemos aplicar el Teorema de Pitágoras en el triángulo de catetos a y l/2 e hipotenusa l para obtener el valor de la apotema a partir del lado:

\ell^2=a^2+\left(\dfrac{\ell}{2}\right)^2\rightarrow a^2=\ell^2-\dfrac{\ell^2}{4}=\dfrac{4\,\ell^2-\ell^2}{4}

a^2=\dfrac{3\,\ell^2}{4}\rightarrow a=\sqrt{\dfrac{3\,\ell^2}{4}}\rightarrow a=\dfrac{\sqrt{3}}{2}\,\ell

EJEMPLO: Calcula la apotema de un hexágono de lado 8 cm.

Sea a la apotema del hexágono, teniendo en cuenta los cálculos anteriores tenemos la siguiente igualdad:

a=\dfrac{\sqrt{3}}{2}\cdot 8=4\sqrt{3}\simeq 6,93

Por lo tanto, la apotema mide aproximadamente 6,93 cm.

Distancias en la circunferencia

Dada una circunferencia de radio r y una cuerda sobre ella de longitud, l, dada, podemos construir un triángulo rectángulo para determinar la distancia de la cuerda al centro de la circunferencia como se ve en la figura:

Se puede aplicar el Teorema de Pitágoras en el triángulo de catetos l/2 y d e hipotenusa r:

r^2=d^2+\left(\dfrac{\ell}{2}\right)^2\rightarrow d=\sqrt{r^2-\dfrac{\ell^2}{4}}

EJEMPLO: En una circunferencia de radio 29 cm se traza una cuerda de 40 cm. ¿Cuál es la distancia del centro de la circunferencia a la cuerda?

Llamamos d a la distancia del centro de la circunferencia a la cuerda, entonces por el Teorema de Pitágoras tenemos la siguiente igualdad:

d=\sqrt{29^2-\dfrac{20^2}{4}}=\sqrt{441}=21

Por lo tanto, la distancia es de 21 cm.

Además de las numerosas aplicaciones a la geometría plana que puede tener el Teorema de Pitágoras, también presenta aplicaciones para la geometría en el espacio. A continuación, se puede ver un ejemplo.

Diagonal de un cubo

Consideramos un cubo de arista a, a partir de la construcción de dos triángulos rectángulos en el se podrá determinar la longitud de su diagonal d, utilizando el Teorema de Pitágoras.

Nuestro objetivo es poder determinar el valor de la diagonal del cubo, D, en función de la longitud del la arista, a.

Para ello se calcula la diagonal de una de las caras, d, y se construye un triángulo rectángulo de catetos a y d e hipotenusa D.

Utilizando el Teorema de Pitágoras en el triángulo rectángulo que aparece punteado en la segunda imagen de la izquierda tenemos:

D^2=a^2+d^2

Pero, si aplicamos el Teorema de Pitágoras en uno de los dos triángulos rectángulos de catetos de longitud a e hipotenusa d que aparecen en la base, tenemos:

d^2=a^2+a^2=2\,a^2

Por lo tanto, podemos sustituir este valor en la anterior expresión para obtener:

D^2=a^2+2\,a^2=3\,a^3\rightarrow D=\sqrt{3\,a^2}=\sqrt{3}\,a

EJEMPLO: Calcula la diagonal de un cubo de arista 5 cm.

Llamamos D a la diagonal del cubo, teniendo en cuenta los cálculos anteriores se tiene la siguiente expresión

D=\sqrt{3}\cdot 5\simeq 8,66

Por lo tanto la diagonal del cubo mide aproximadamente 8,66 cm.