Para continuar aprendendo os trazados e construccións básicas do debuxo técnico e como continuación da unidade 7 (Arréglome), imos estudalos polígonos e as súas características.
Un polígono é unha figura plana e pechada limitada por una liña crebada. Cada segmento da liña crebada denomínase lado, e os puntos de intersección dos lados chámanse vértices.
Se tódolos lados son iguais o polígono chámase equilátero; se os ángulos son iguais, chámase equiángulo; se os lados e os ángulos son iguais, o polígono chámase regular; no caso contrario denomínanse polígonos irregulares. A suma dos ángulos externos dun polígono é igual a 360 graos.
O polígono ten as seguintes liñas notables:
Radio: é a recta R que vai desde o centro a un vértice calquera.
Apotema: é a recta a que une o centro co punto medio de un dos seus lados.
Altura: é a recta h perpendicular a un dos lados trazada desde o vértice oposto.
Diagonal principal: nos polígonos dun número par de lados, é a recta d que une dous vértices opostos.
Perímetro: é a suma das lonxitudes de tódolos lados do polígono.Este é o nome dos polígonos segundo o número de lados:
3 lados triángulo
4 lados cadrado
5 lados pentágono
6 lados hexágono
7 lados heptágono
8 lados octógono
9 lados eneágono
10 lados decágono
11 lados undecágono
12 lados dodecágono
Éstas son as construcións particulares dos polígonos, coñecendo o radio da circunferencia que o circunscribe.
Construción do triángulo inscrito nunha circunferencia de radio coñecido.
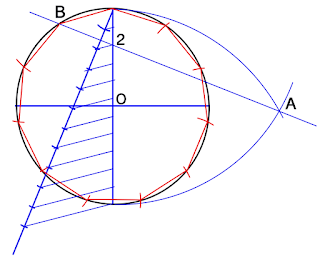
Método xeral de construción de polígonos inscrito nunha circunferencia de radio coñecido.
Ademais de todos estes métodos temos unha maneira xeral coa que podemos construír poligonos con calquera número de lados.
A construción de polígonos xa foi vista en cursos anteriores, polo que resultará sinxelo recordarlos pasos vendo os debuxos. Aínda que se hai algunha dúbida, temos no youtube feixes de explicacións sobre calquera procedemento. Ou plataformas adicadas ó debuxo como por exemplo a de Mongge. Nestos enlaces tes algún exemplo:
Ademais de todos estes métodos temos unha maneira xeral coa que podemos construír poligonos con calquera número de lados.
A construción de polígonos xa foi vista en cursos anteriores, polo que resultará sinxelo recordarlos pasos vendo os debuxos. Aínda que se hai algunha dúbida, temos no youtube feixes de explicacións sobre calquera procedemento. Ou plataformas adicadas ó debuxo como por exemplo a de Mongge. Nestos enlaces tes algún exemplo:
www.mongge.com/ejercicios/1974
www.mongge.com/ejercicios/28118
www.mongge.com/ejercicios/23857
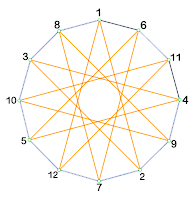
Ademáis dos polígonos coñecidos, poderemos construír tamén os polígonos estrelados, unha vez que os vértices quedan marcados na circunferencia só teremos que cambiar a forma de unilos.
Se unimos os vértices dun polígono saltando rítmicamente un número dado de vértices (ó que chamamos paso) ata volver ao primeiro conseguiremos un polígono estrelado. Dependendo do número de vértices poderemos conseguir máis ou menos polígonos estrelados cun mesmo número de puntas.
Se o número de vértices que imos saltando é divisor do número de lados, a estrela que obtemos non é un polígono estrelado verdadeiro, senón a intersección de outros polígonos menores superpostos. O cal sería un polígono dun número de lados igual ó número de lados do orixinal dividido entre o paso. Observa o exemplo:
Neste video podes ver os fermosos motivos decorativos da arte islámica, deseñadas a partir de diversas relacións entre elementos xeométricos e formas poligonais. https://youtu.be/pg1NpMmPv48
www.mongge.com/ejercicios/28118
www.mongge.com/ejercicios/23857
Neste video podes ver os fermosos motivos decorativos da arte islámica, deseñadas a partir de diversas relacións entre elementos xeométricos e formas poligonais. https://youtu.be/pg1NpMmPv48