Os sistemas de representación constitúen o instrumento gráfico usado para os traballos de debuxo técnico e deseño. Engloba 3 sistemas diferentes, o diédrico a perspectiva axonométrica e a perspectiva cónica. É unha linguaxe universal que pode ser comprendida en calquera momento e en todo o mundo.
Imaxe de creación propia
O estudo científico da perspectiva é relativamente recente na historia humana xa que non se formulou con precisión ata o Renacemento Italiano, no século XV. Pasaron varios séculos ata que no 1400 se comezou a desenvolver unha idea consistente nos puntos de fuga, alcanzando unha comprensión intuitiva da perspectiva. O arquitecto florentino Brunelleschi foi quen superou as leis da mesma a través dunha serie de experimentos que realizou. Varios pintores deste período artístico aplicaron as regras de Brunelleschi para conseguir o efecto de perspectiva na pintura.
Imaxe de dominio público. Rescatada da Wikipedia
A Xeometría Descritiva é a ciencia que ten por obxecto a representación de figuras e obxectos tridimensionais no plano (espazo bidimensional). O elemento mínimo de representación en calquera sistema é o punto e para poder proxectalo trázase unha recta (raio proyectante) por el, cumprindo unha serie de condicións, e calcúlase a intersección deste raio co plano sobre o cal se desexa proxectar (plano do cadro).
O número de planos de proxección utilizados, a situación relativa destos respecto ó obxecto, e a dirección dos raios proxectantes, son as características que diferencian ós distintos sistemas de representación.
Proxección cónica
Se o punto de vista ou vértice da radiación é un punto propio (está na zona finita do espazo), o feixe proxectivo ten forma cónica, resultando o Sistema Cónico. Este é o máis empregado usualmente en arte, así como en arquitectura e enxeñería, principalmente cando se trata de representar edificios nos que interesa unha percepción máis realista do obxecto.
Proxección cilíndrica
Se o punto de vista está no infinito, os raios proxectivos son paralelos. A estes sistemas denomínaselles de proxección cilíndrica ou paralela e teñen importantes vantaxes debido a que simplifican a representación. Se estes raios proxectivos son perpendiculares ao plano de proxección, dise que o sistema de representación é ortogonal, en caso contrario é oblicuo.
Imaxe de creación propia
Sistema diédrico
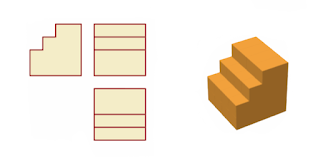
O sistema diédrico consiste na representación gráfica dun obxecto en planta e alzado, mediante a proxección de raios proxectantes perpendiculares a dous planos principais de proxección denominados plano horizontal (PH) e plano vertical (PV). O obxecto queda representado pola súa vista frontal (proxección no plano vertical) e a súa vista superior (proxección no plano horizontal); tamén se pode representar a súa vista lateral, como proxección auxiliar. A estas dúas proxeccións adoitaselles chamar no debuxo técnico alzado e planta. A terceira vista, a vista lateral chámase perfil.
No debuxo vemos as 3 vistas por separado, o alzado, que é a vista principal, e a planta xusto debaixo. O perfil colócase ó lado do alzado. Como se pode ver, o perfil colócase no lado contrario do que se ve na figura (dacordo ó Sistema Europeo).
Ademais dos dous plano proxectantes, son importantes tamén os dous planos bisectores.
Imaxe de creación propia
Un punto situado no espazo represéntase mediante as súas dúas proxeccións sobre os planos de proxección.
Cota: Denomínase cota dun punto do espazo á distancia entre el e a súa proxección no plano horizontal.
Afastamento: Denomínase afastamento dun punto do espazo á distancia que hai entre el e a súa proxección no plano vertical.
Podemos coñecer un punto polas súas coordenadas; por exemplo P(O,A,C) onde O é a distancia a un punto que representaa ao orixe, A o afastamento e C a cota.
Para representar un punto de maneira gráfica, o primeiro é debuxar as súas dúas proxeccións sobre os planos. Teremos que abater (superpoñer) os dous planos para que nos quede en dúas dimensións e logo debuxar as súas proxeccións sobre os planos. Na figura temos á dereita o punto colocado no espazo e as súas proxeccións sobre os dous planos. Á esquerda vemos a representación sobre o papel unha vez xa abatidos os planos.
Trazas da recta
Son os puntos onde a recta corta aos planos de Proxección. Pola súa posición particular haberá algunhas rectas que teñen dúas, unha ou ningunha traza. Traza horizontal da recta ( h´, h´´) é o punto onde a recta corta ó plano horizontal. Traza vertical da recta (v´, v´´) é o punto onde a recta corta ao plano vertical. Enténdese que unha recta cambia de cadrante cando atravesa algún dos planos de proxección. Desta forma, as trazas determinan os cambios de diedro dunha recta. Tamén nos indican as partes vistas e ocultas da recta, pois considérase que esta é vista unicamente cando pasa polo primeiro cadrante.
Posicións de rectas en relación ós planos de proxeción:
Imaxe de creación propia
a. Recta horizontal; b. recta frontal; c. Recta vertical; d. Recta de punta; e. Recta oblicua; f. Recta que corta á liña de terra; g. Recta de perfil; h. Recta paralela a ambos planos de proxección.
Representación dun Plano
Xeralmente entendemos que unha superficie plana é aquela que pode conter unha recta imaxinaria en calquera dirección. Así pois, as caras dunha forma, obxecto, poliedro, etc., son planos delimitados por rectas e vértices (puntos). No sistema diédrico entendemos que un plano é unha superficie plana infinita e ilimitada. Para definir un plano necesitamos os seguintes elementos xeométricos: tres puntos calquera que non estean aliñados, unha recta e un punto exterior a ela, dúas rectas que se cortan e dúas rectas paralelas. Un plano represéntase mediante as súas trazas. As trazas dun plano son as rectas de intersección do plano cos planos de proxección.
Unha recta pertence a un plano cando os seus puntos traza están contidos nas trazas do plano. Un punto pertence a un plano cando está contido nunha recta que pertence ao plano.
Imaxe de creación propia
Plano proxectante horizontal: é perpendicular ó plano de proxección horizontal. A traza horizontal forma un ángulo calquera coa liña de terra. Ten a traza vertical perpendicular á liña de terra. A proxección horizontal de todo punto ou recta contidos no plano atoparase contido na traza horizontal do plano.
Plano proxectante vertical: é perpendicular ao plano de proxección vertical. Ten a traza horizontal perpendicular á liña de terra. A traza vertical forma un ángulo calquera coa liña de terra. Calquera punto ou recta contido no plano terá a súa proxección vertical contida na traza vertical do plano.
Plano de perfil: este plano é perpendicular a ambos os Planos de Proxección. Ten ambas Trazas perpendiculares á Liña de Terra. Calquera punto ou recta contidos no plano terán as súas proxección contidas nas Trazas do Plano. Para poder traballar con puntos ou rectas contidos neste plano faremos uso dunha terceira vista de perfil, onde poderemos ver os elementos contidos no plano en verdadeira magnitude.
Plano horizontal: é paralelo ao plano de proxección horizontal ( PH). Polo tanto, ten só traza vertical e esta é paralela á liña de terra. Os elementos contidos neste plano teñen a súa proxección vertical contida na traza do plano e a súa proxección horizontal vese en verdadeira magnitude.
Plano frontal: é paralelo ao plano de proxección vertical ( PV). Só ten traza horizontal e esta é paralela á liña de terra. Calquera punto ou recta contido neste plano terá a súa proxección horizontal contida na traza do plano e verase en verdadeira magnitude en proxección vertical.
Plano paralelo a LT: ten tanto traza horizontal como vertical. Ambas son paralelas á liña de terra, polo que non se cortan (ou se cortan no infinito). A distancia das trazas á liña de terra define a inclinación e posición do plano. Para ver a inclinación do plano en verdadeira magnitude utilízase unha vista de perfil, como no caso do plano de perfil, mencionado 3 apartados máis arriba.
Plano que pasa por LT: este plano ten só unha traza superposta á liña de terra. Para poder ser definido completamente é necesario dar polo menos un punto pertencente ao plano. Desta maneira pódese utilizar unha vista auxiliar de perfil para entender completamente o plano e ver a súa inclinación en verdadeira magnitude.
Segundo a posición dos eixos, distinguimos entre varias perspectivas axonométricas diferentes, que son, a Isométrica, a Cabaleira e a Militar.
Perspectiva Isométrica, onde os tres ángulos son de 120º
Perspectiva Militar onde os eixos que forman o plano horizontal, OX e OY, forman 90º. Con respeto do eixo Z pódense colocar libremente.
A principal vantaxe é que as distancias no plano horizontal conservan as súas dimensións e proporcións. As circunferencias no plano horizontal pódense trazar con compás, pois non presentan deformación. As circunferencias nos planos verticais represéntanse como elipses. A perspectiva militar sería como observalo corpo desde arriba, pois é a única forma de que os eixos X e E presenten 90°.
O sistema cónico é un sistema de representación gráfico baseado na proxección dun corpo tridimensional sobre un plano, mediante rectas proxectantes que pasan por un punto; lugar desde o cal se supón que mira o observador. O resultado final é unha representación no plano da visión realista obtida cando o ollo está no devandito punto, lugar desde o cal aumenta a sensación de estar dentro da imaxe representada.
Imaxe de creación propia
PUNTO DE VISTA (V): é o centro da proxección e sinala a posición do ollo do observador.
PLANO DO CADRO (PC): sobre el proxéctase o obxecto. É un plano vertical e pódese colocar entre o observador e o obxecto, no obxecto ou detrás do obxecto.
PUNTO PRINCIPAL (PP): é a proxección ortogonal do punto de vista sobre o PC.
PLANO XEOMETRAL (PX): sobre el sitúanse os obxectos que se van a representar.
LIÑA DO HORIZONTE (LH): é a intersección do PC co PH.
DISTANCIA PRINCIPAL: é a distancia entre o punto de vista e o punto principal.
PUNTO DE FUGA: é un punto no infinito situado na liña de horizonte.
Na frontal os obxectos sitúanse coas súas caras paralelas ao plano do cadro. Hai un só punto de fuga, que está situado na liña do horizonte e coincide co punto principal P.
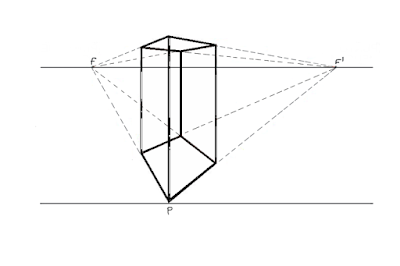
Na oblicua as caras da figura están oblicuas con respecto do plano do cadro. Neste caso hai dous puntos de fuga situados sobre a liña do horizonte, F e F´.